UNIDAD #1
1.1 LA NATURALEZA DE LA FÍSICA
Es una de las ciencias que a contribuido al desarrollo de la humanidad, porque gracias a los estudios ye investigaciones a sido posible encontrar explicaciones a diferentes fenómenos de la naturaleza, ejemplo.- En nuestra vida cotidiana vemos como los objetos por efecto de la gravedad se mantienen en el suelo. son cosas que por leyes de la física suceden.
1.2 SÍMBOLO DE LA UNIDADES
se trata de comprender unas pocas normas sencillas para reconocer, no lleva punto a no ser que se encuentre al final de una frase. no se trata de una abreviatura, si no de una identidad matemática, eso significa que nunca lo ponemos en plural ni cambiaremos una minúscula por una mayúscula, o viceversa, el sistema internacional de unidades fue adoptado por la conferencia general de pesos y magnitudes en 1960, solo hay tres países que lo han adoptado oficialmente: Liberia, Birmania y Estados Unidos, y consta de dos tipos de unidades; básicas y derivadas.
UNIDADES BÁSICAS
|
Magnitud
|
Unidades
|
Símbolo
|
Longitud
|
Metro
|
m
|
Masa
|
Kilogramo
|
Kg
|
Tiempo
|
Segundo
|
s
|
UNIDADES
DERIVADAS DEL S.I
|
Magnitudes
|
Nombre
|
Símbolo
|
Relación con las unidades
básicas
|
Superficie/Área
|
Metro cuadrado
|
m2
|
m2
|
Volumen
|
Metro cúbicos
|
m3
|
m3
|
Velocidad
|
por segundo cuadrado
|
m/s
|
m/s
|
Aceleración
|
Metro por segundo cuadrado
|
m/s2
|
m/s2
|
velocidad angular
|
Radian por segundo
|
rad/s
|
s-1
|
Fuerza
|
Newton
|
N
|
Kg.m/s2
|
Presión
|
Pascal
|
Pa
|
N/m2
|
Energía/Trabajo
|
Joul
|
J
|
N.m
|
Flujo
|
Caudal
|
m3/s
|
m3/s
|
Potencia
|
Watt
|
W
|
J/s
|
1.2.3 SISTEMA DE UNIDADES
Los sistemas de unidades son conjuntos de unidades convenientemente relacionadas entre sí que se utilizan para medir diversas magnitudes (longitud, peso, volumen, etc.). Universalmente se conocen tres sistemas de unidades: Las unidades correspondientes a las magnitudes (longitud, tiempo y masa) expresadas en cada uno de estos sistemas, se presentan a continuación.
Unidades de longitud
Las unidades de longitud permiten medir el largo, ancho y alto de diferentes objetos, es decir, medidas en una sola dimensión. En el sistema internacional, la unidad de las medidas de longitud es el metro, representado por la letra m. Los submúltiplos del metro se obtienen anteponiendo a la palabra metro los prefijos: deci, centi y mili, que significan décima, centésima y milésima parte. Sirven para medir longitudes menores que el metro. Los múltiplos se forman anteponiendo los prefijos: kilo, hecto y deca, que significan mil, cien y diez respectivamente. Se utilizan para longitudes mayores que el metro.
Km
|
hm
|
dam
|
m
|
dm
|
cm
|
mm
|
kilometro
|
hectómetro
|
decametro
|
metro
|
decimetro
|
centimetro
|
milimetro
|
Unidades de masa
En el sistema cgs, la unidad fundamental es el gramo, que se simboliza con la letra g. Sus múltiplos y submúltiplos se presentan en la siguiente tabla. El tratamiento de los datos es equivalente al utilizado para las unidades de longitud.
Kg
|
hg
|
dag
|
g
|
dg
|
cg
|
mg
|
Kilogramo
|
hectagramo
|
decagramo
|
gramo
|
decigramo
|
centigramo
|
miligramo
|
Unidades de superficie
La unidad convencional de superficie es el metro cuadrado (m2). Un metro cuadrado es la superficie de un cuadrado que tiene 1 m x 1m. Al igual que para el resto de las unidades estudiadas, existen múltiplos y submúltiplos del m2.
1.4 PREFIJOS DE UNIDADES
Los prefijos del SI para nombrar a los múltiplos y submúltiplos de cualquier unidad del Sistema Internacional (SI), ya sean unidades básicas o derivadas. Estos prefijos se anteponen al nombre de la unidad para indicar el múltiplo o submúltiplo decimal de la misma; del mismo modo, los símbolos de los prefijos se anteponen a los símbolos de las unidades.
1000n
|
10n
|
Prefijo
|
Símbolo
|
|
|
Equivalencia decimal en los Prefijos del
Sistema Internacional
|
Asignación
|
10008
|
1024
|
|
Y
|
|
|
1 000 000 000
000 000 000 000 000
|
1991
|
10007
|
1021
|
|
Z
|
|
Mil trillones
|
1 000 000 000
000 000 000 000
|
1991
|
10006
|
1018
|
|
E
|
|
|
1 000 000 000
000 000 000
|
1975
|
10005
|
1015
|
|
P
|
|
Mil billones
|
1 000 000 000
000 000
|
1975
|
10004
|
1012
|
|
T
|
|
|
1 000 000 000
000
|
1960
|
10003
|
109
|
|
G
|
|
|
1 000 000 000
|
1960
|
10002
|
106
|
|
M
|
|
1 000 000
|
1960
|
10001
|
103
|
|
k
|
|
1 000
|
1795
|
10002/3
|
102
|
|
h
|
|
100
|
1795
|
10001/3
|
101
|
|
da
|
|
10
|
1795
|
10000
|
100
|
ninguno
|
|
1
|
|
1000−1/3
|
10−1
|
|
d
|
Décimo
|
0,1
|
1795
|
1000−2/3
|
10−2
|
|
c
|
Centésimo
|
0,01
|
1795
|
1000−1
|
10−3
|
|
m
|
Milésimo
|
0,001
|
1795
|
1000−2
|
10−6
|
|
µ
|
|
0,000 001
|
1960
|
1000−3
|
10−9
|
|
n
|
Billonésimo
|
Milmillonésimo
|
0,000 000 001
|
1960
|
1000−4
|
10−12
|
|
p
|
Trillonésimo
|
Billonésimo
|
0,000 000 000
001
|
1960
|
1000−5
|
10−15
|
|
f
|
Cuatrillonésimo
|
Milbillonésimo
|
0,000 000 000
000 001
|
1964
|
1000−6
|
10−18
|
|
a
|
Quintillonésimo
|
Trillonésimo
|
0,000 000 000
000 000 001
|
1964
|
1000−7
|
10−21
|
|
z
|
Sextillonésimo
|
Miltrillonésimo
|
0,000 000 000
000 000 000 001
|
1991
|
1000−8
|
10−24
|
|
y
|
Septillonésimo
|
Cuatrillonésimo
|
0,000 000 000
000 000 000 000 001
|
1991
|
1.5 NOTACIÓN CIENTÍFICA
La notación científica (o notación índice estándar) es una manera rápida de representar un número utilizando potencias de base diez. Esta notación se utiliza para poder expresar muy fácilmente números muy grandes o muy pequeños.
Los números se escriben como un producto:
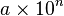
siendo:
-
1.6 CIFRAS SIGNIFICATIVAS
Reglas para establecer las cifras significativas de un número dado.
Regla 1. En números que no contienen ceros, todos los dígitos son significativos.
Por ejemplo:
3,14159 → seis cifras significativas → 3,14159
|
5.694 → cuatro cifras significativas → 5.694
|
Regla 2. Todos los ceros entre dígitos significativos son significativos.
Por ejemplo:
2,054 → cuatro cifras significativas → 2,054
|
506 → tres cifras significativas → 506
|
Regla 3. Los ceros a la izquierda del primer dígito que no es cero sirven solamente para fijar la posición del punto decimal y no son significativos.
Por ejemplo:
0,054 → dos cifras significativas → 0,054
|
0,0002604 → cuatro cifras significativas → 0,0002604
|
Regla 4. En un número con dígitos decimales, los ceros finales a la derecha del punto decimal son significativos.
Por ejemplo:
0,0540 → tres cifras significativas → 0,0540
|
30,00 → cuatro cifras significativas → 30,00
|
Regla 5. Si un número no tiene punto decimal y termina con uno o más ceros, dichos ceros pueden ser o no significativos. Para poder especificar el número de cifras significativas, se requiere información adicional. Para evitar confusiones es conveniente expresar el número en notación científica, no obstante, también se suele indicar que dichos ceros son significativos escribiendo el punto decimal solamente. Si el signo decimal no se escribiera, dichos ceros no son significativos.
Por ejemplo:
1200 → dos cifras significativas → 1200
|
1200, → cuatro cifras significativas → 1200,
|
Regla 6. Los números exactos tienen un número infinito de cifras significativas.
Los números exactos son aquellos que se obtienen por definición o que resultan de contar un número pequeño de elementos. Ejemplos:
- Al contar el número de átomos en una molécula de agua obtenemos un número exacto: 3.
- Al contar las caras de un dado obtenemos un número exacto: 6.
- Por definición el número de metros que hay en un kilómetro es un número exacto: 1000.
- Por definición el número de grados que hay en una circunferencia es un número exacto: 360
1.7 ANÁLISIS DIMENSIONAL
Es una herramienta que permite simplificar el estudio de cualquier fenómeno en el que estén involucradas muchas magnitudes físicas en forma de variables independientes, permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada dimensionales más reducido. Estos parámetros dimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada sistema.
1.8 CONVERSIONES DE UNIDADES
Son las transformaciones de una magnitud
física, expresada en una cierta unidad
de medida, en otra equivalente, que puede ser del mismo sistema de unidades o
no. Este proceso suele realizarse con el uso de los factores de conversión y las tablas
de conversiones en la física
Frecuentemente basta multiplicar por
una fracción (factor
de una conversión) y el resultado es otra medida equivalente, en la que han
cambiado las unidades. Cuando el cambio de unidades implica la transformación
de varias unidades se pueden utilizar varios factores de conversión uno tras
otro, de forma que el resultado final será la medida equivalente en las
unidades que buscamos, por ejemplo si queremos pasar 8 metros a yardas, lo primero que
tenemos que hacer, es conocer cuánto vale una yarda en metros para poder
transformarlo, en donde, una yarda(yd)= 0,914m, luego dividir 0,914 entre 8 y
nos daría como resultado 0,11425yardas
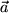 obtenemos el vector unitario en la dirección del vector dividiendo por su longitud
obtenemos el vector unitario en la dirección del vector dividiendo por su longitud , o multiplicando por
, o multiplicando por 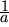 :
: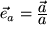 o
o 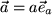 .
. si y solamente si el módulo de v es igual a 1 O en forma más compacta:
si y solamente si el módulo de v es igual a 1 O en forma más compacta: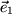 ,
, 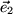 y
y 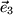 como vectores base , donde
como vectores base , donde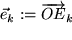 . Algunas veces los tres vectores base
. Algunas veces los tres vectores base 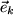 normalizados a uno también se denominan un triedro.
normalizados a uno también se denominan un triedro.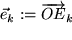 son perpendiculares entre sí de a pares, y luego forman una base ortonormal, BON (es decir, ortogonal y normalizada). Para expresar esto en fórmula, necesitamos una cantidad conectada con el ángulo entre dos vectores, que dice, por ejemplo, que con un ángulo recto entre ellos, la proyección de un vector sobre el otro desaparece. Esta tarea nos conduce a la pregunta acerca de la multiplicación de dos vectores, que veremos en la siguiente sección.
son perpendiculares entre sí de a pares, y luego forman una base ortonormal, BON (es decir, ortogonal y normalizada). Para expresar esto en fórmula, necesitamos una cantidad conectada con el ángulo entre dos vectores, que dice, por ejemplo, que con un ángulo recto entre ellos, la proyección de un vector sobre el otro desaparece. Esta tarea nos conduce a la pregunta acerca de la multiplicación de dos vectores, que veremos en la siguiente sección.