1.- VECTORES EN TRES DIMENSIONES
Se sabe que los vectores tienen módulo o magnitud y dirección. Un vector ubicado en un sistema de coordenadas rectangulares puede ser expresado como coordenadas o con una ecuación vectorial donde intervienen unos vectores muy especiales: i, j y k. denominados vectores unitarios. El uso de estos vectores unitarios hace que las operaciones vectoriales como la suma, resta e inclusive producto sean mucho más fácil.
Vectores en Tres Dimensiones (Teoría)
Los vectores pueden expresarse en función de
o de otra forma:
donde: i j k
son vectores denominados,
vectores unitarios que indican la dirección de
los ejes “x”, “y”, “z” respectivamente.
El módulo del vector A es igual:
SUMA DE VECTORES
Si se tiene:
Entonces:
RESTA DE VECTORES
Si se tiene:
Entonces:
PRODUCTO DE VECTORES
Producto escalar
Al multiplicar escalarmente dos vectores, se obtiene como resultado “un número”. Dicho número se obtiene multiplicando los módulos de los vectores y por el coseno del ángulo que forman dichos vectores.
Producto vectorial
Al multiplicar vectorialmente dos vectores se obtiene como resultado a otro vector. El módulo de ese vector es igual al producto de los módulos de los vectores a multiplicar y por seno del ángulo que forman entre sí.
La dirección de dicho vector es perpendicular
al plano que contiene a los vectores A
y B
Si los vectores A y B son dados de la siguiente forma:
A = (1;3;2) y B = (4;5;6)
Su productor vectorial se determina así:
Si se desea calcular el módulo del producto vectorial se procede a efectuar así:
¿Cómo se determina el vector unitario de un vector?
El vector unitario de cualquier vector se expresa de la siguiente manera:
2.- VECTOR UNITARIO
En ocasiones se le llama también vector normalizado.
Vectores unitarios son vectores adimensionales de longitud 1. Cada vector unitario especifica una dirección en el espacio. A partir de cualquier vector 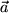 obtenemos el vector unitario en la dirección del vector dividiendo por su longitud
obtenemos el vector unitario en la dirección del vector dividiendo por su longitud , o multiplicando por
, o multiplicando por 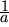 :
:
vector unitario: 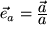 o
o 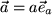 .
.
Definición
Habiendo definido el concepto de vector unitario al comienzo de este artículo y habiendo presentado la notación usual en la sección anterior, presentamos en esta sección una definición simbólica de vector unitario.
- Sea el vector v ∈ ℝn. Se dice que v es un vector unitario y se lo denota mediante
 si y solamente si el módulo de v es igual a 1 O en forma más compacta:
si y solamente si el módulo de v es igual a 1 O en forma más compacta:
En lo que sigue usaremos los tres vectores unitarios 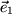 ,
, 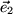 y
y 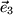 como vectores base , donde
como vectores base , donde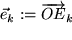 . Algunas veces los tres vectores base
. Algunas veces los tres vectores base 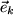 normalizados a uno también se denominan un triedro.
normalizados a uno también se denominan un triedro.
Después de que hemos introducido las componentes de los vectores como desplazamientos parciales a lo largo de los ejes coordenados (o equivalentemente como proyecciones de la longitud del vector sobre los ejes coordenados), se sigue directamente:
Dado que hemos seleccionado un sistema de coordenadas Cartesiano al comienzo de este capítulo, sabemos que los tres vectores unitarios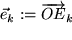 son perpendiculares entre sí de a pares, y luego forman una base ortonormal, BON (es decir, ortogonal y normalizada). Para expresar esto en fórmula, necesitamos una cantidad conectada con el ángulo entre dos vectores, que dice, por ejemplo, que con un ángulo recto entre ellos, la proyección de un vector sobre el otro desaparece. Esta tarea nos conduce a la pregunta acerca de la multiplicación de dos vectores, que veremos en la siguiente sección.
son perpendiculares entre sí de a pares, y luego forman una base ortonormal, BON (es decir, ortogonal y normalizada). Para expresar esto en fórmula, necesitamos una cantidad conectada con el ángulo entre dos vectores, que dice, por ejemplo, que con un ángulo recto entre ellos, la proyección de un vector sobre el otro desaparece. Esta tarea nos conduce a la pregunta acerca de la multiplicación de dos vectores, que veremos en la siguiente sección.














